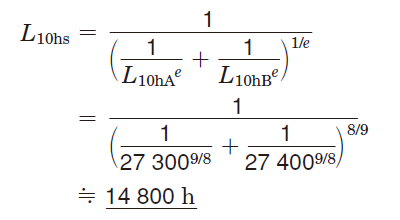[Example 1] Bearing service life (time) with 90 % reliability
(Conditions)
Deep groove ball bearing : 6308
Radial load Fr=3500 N
Axial load not applied(Fa = 0)
Rotational speed n=800min-1
①Basic dynamic load rating (Cr) is obtained from the bearing specification table.
Cr = 50.9 kN
②Dynamic equivalent radial load (Pr) is calculated using equation (5-32).
Pr = Fr = 3500 N
③Bearing sevice life (L10h) is calculated using equation (5-2).
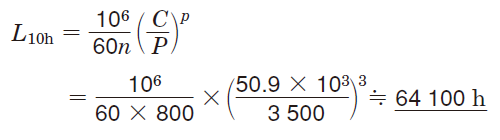
[Example 2] Bearing service life (time) with 96 % reliability
(Conditions)
Deep groove ball bearing : 6308
Radial load Fr= 3500N
Axial load Fa= 1000N
Rotational speed n= 800min-1
①From the bearing specification table ;
Basic load rating (Cr, C0r) ƒ0 factor is obtained.
Cr = 50.9 kN
ƒ0 = 13.2
C0r = 24.0 kN
Values X and Y are obtained by comparing value e, calculated from value ƒ0 Fa / C0r via proportional interpolation, with value ƒ0 Fa / Fr.
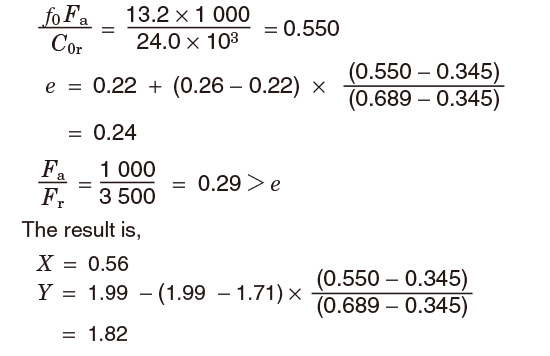
②Dynamic equivalent load (Pr) is obtained using equation (5-32).
Pr = XFr + YFa =(0.56 × 3500)+(1.82 × 1000)=3780 N
③Service life with 90 % reliability (L10h) is obtained using equation (5-2).
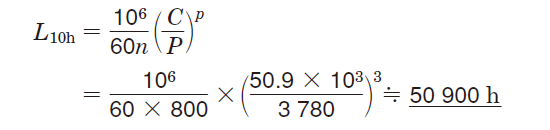
[Example 3] Calculation of the αISO factor with the conditions in Example 2
(Conditions)
Oil lubrication (Oil that has been filtered by a fine filter)
Operating temperature 70℃
96% reliability
④Lubricating oil selection
From the bearing specification table, the pitch diameter Dpw = (40 + 90)/2 = 65 is obtained.
dmn = 65 × 800 = 52 000. Therefore, select VG 68 from Table 12-8, Proper kinematic viscosities by bearing operating conditions.
⑤Calculating the αISO factor
The operating temperature is 70 °C, so according to Fig. 12-3, Relationship between lubricating oil viscosity and temperature (viscosity index :100), the viscosity when operating is ν = 20 mm2/s
According to Fig. A, ν1 = 21.7 mm2
κ = ν / ν1 = 20/21.7 = 0.92
The oil has been filtered by a fine filter, so Table 5-4 shows ec is 0.5 to 0.6.
To stringently estimate the value, ec = 0.5.
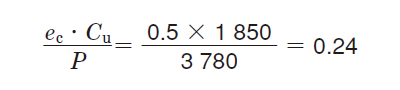
Therefore, according to Fig. B
αISO = 7.7
⑥Service life with 96 % reliability (Lnm) is obtained using equation (5-8).
According to Table 5-3, α1 = 0.55.
L4m= α1αISOL10 = 0.55× 7.7 ×50900≒ 216000 h
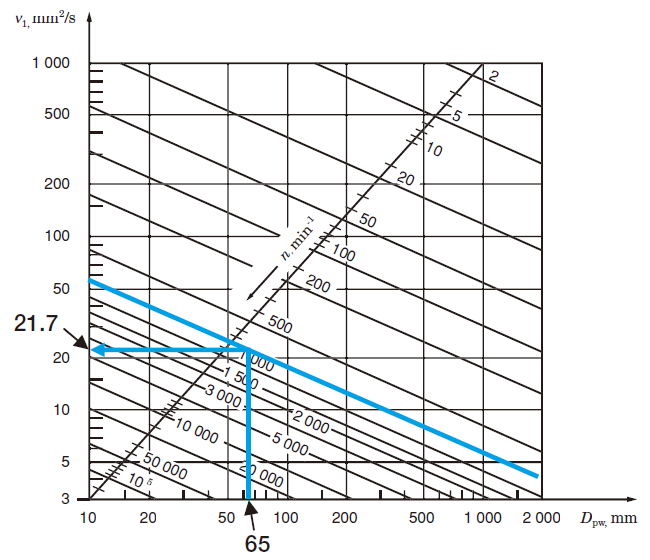
Fig. A
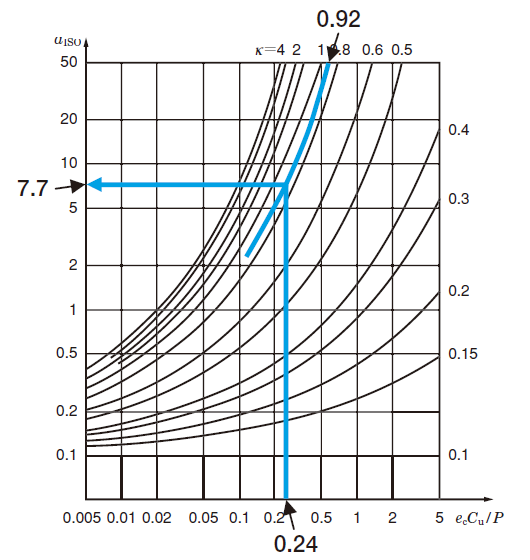
Fig. B
The αISO factor can also be calculated on our website.
Click here to WEB based technical calculation tool
[Example 4] Bearing service life (total revolution)
(Conditions)
Tapered roller bearing
Bearing A:30207 JR
Bearing B:30209 JR
Radial load
FrA= 5200 N
FrB= 6800 N
Axial load Ka= 1600 N
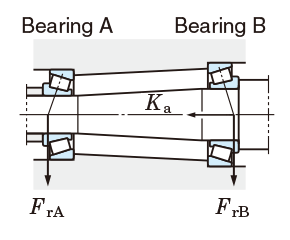
①From the bearing specification table, the following specifications are obtained.
| Basic dynamic load rating (Cr) | e | X1) | Y1) | |
|---|---|---|---|---|
| Bearing A | 68.8 kN | 0.37 | 0.4 | 1.60 |
| Bearing B | 83.9 kN | 0.40 | 0.4 | 1.48 |
[Note] 1) Those values are used, where Fa/Fr> e.
Where Fa/Fr≦ e, X= 1,Y= 0.
②Axial load applied to shafts must be calculated, considering the fact that component force in the axial direction is generated when radial load is applied to tapered roller bearings.
(ref. equation 5-33, Table 5-9)
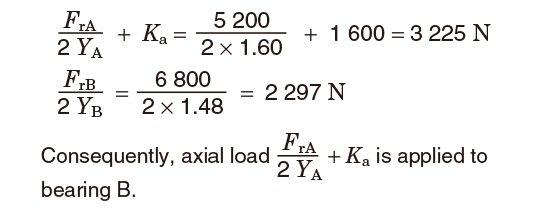
③Dynamic equivalent load (Pr) is obtained from Table 5-9.
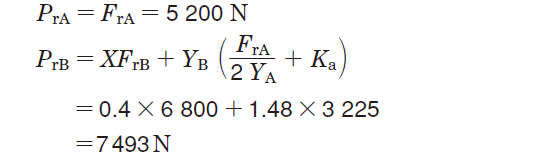
④Each bearing service life (L10) is calculated using equation (5-1).
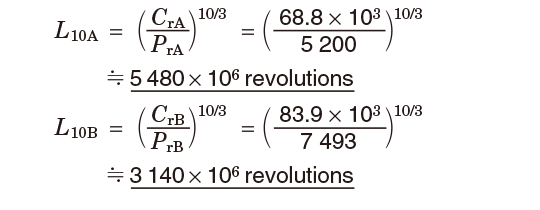
[Example 5] Bearing size selection
(Conditions)
Deep groove ball bearing : 62 series
Required service life : more than 10000 h
Radial load Fr= 2000 N
Axial load Fa= 300 N
Rotational speed n = 1600 min-1
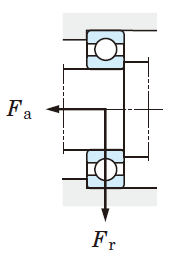
①The dynamic equivalent load (Pr) is hypothetically calculated.
The resultant value, Fa / Fr = 300/2000 = 0.15, is smaller than any other values of e in the bearing specification table.
Hence, JTEKT can consider that Pr = Fr = 2000 N.
②The required basic dynamic load rating (Cr) is calculated according to equation (5-4).
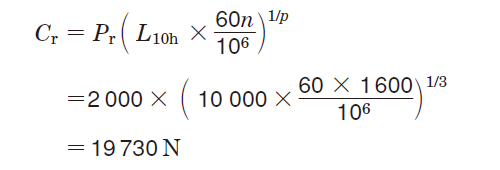
③Among those covered by the bearing specification table, the bearing of the 62 series with Cr exceeding 19730 N is 6205R, with bore diameter for 25 mm.
④The dynamic equivalent load obtained at step ① is confirmed by obtaining value e for 6205 R.
Where C0r of 6205 R is 9.3 kN, and ƒ0 is 12.8
ƒ0 Fa/C0r = 12.8 × 300/9300 = 0.413
Then, value e can be calculated using proportional interpolation.
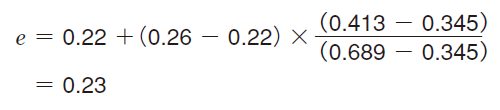
As a result, it can be confirmed that
Fa / Fr = 0.15 < e.
Hence, Pr = Fr.
[Example 6] Bearing size selection
(Conditions)
Deep groove ball bearing : 63 series
Required service life : more than 15 000 h
Radial load Fr = 4000 N
Axial load Fa= 2400 N
Rotational speed n = 1000 min-1
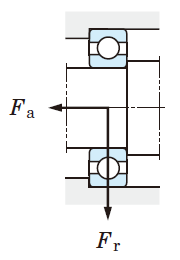
①The hypothetic dynamic equivalent load (Pr) is calculated :
Since Fa/Fr = 2400/4000 = 0.6 is much larger than the value e specified in the bearing specification table, it suggests that the axial load affects the dynamic equivalent load.
Hence, assuming that X = 0.56, Y = 1.6
(approximate mean value of Y), using equation (5-32),
Pr = XFr + XFa = 0.56 × 4000 + 1.6 × 2400 = 6080 N
②Using equation (5-4), the required basic dynamic load rating (Cr) is :
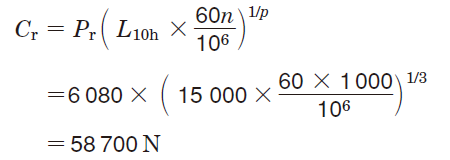
③From the bearing specification table, a 6309 with a bore diameter of 45 mm is selected as a 63 series bearing with Cr exceeding 58700 N.
④The dynamic equivalent load and basic rating life are confirmed, by calculating the value e for a 6309.
Values obtained using the proportional interpolation are :
where ƒ0Fa/C0r = 13.3 × 2400/29500 = 1.082
e = 0.283, Y = 1.54.
Thus, Fa / Fr = 0.6 > e.
Using the resultant values, the dynamic equivalent load and basic rating life can be calculated as follows :
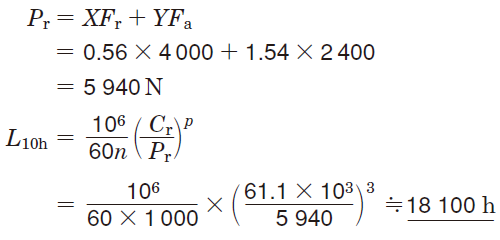
⑤The basic rating life of the 6308, using the same steps, is :
L10h ≒ 11500 h, which does not satisfy the service life requirement.
[Example 7] Calculation of allowable axial load for cylindrical roller bearings
(Conditions)
Single-row cylindrical roller bearing : NUP 310
Rotational speed n = 1500 min-1
Oil lubrication
Axial load is intermittently applied.
①Using the bearing specification table, the value dm for the NUP 310 can be calculated as follows :
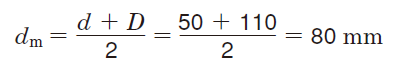
②Each coefficient used in equation (5-45).
From values listed in Table 5-11, coefficient ƒa related to intermittent load is : ƒa = 2
From values listed in Table 5-12, coefficient ƒb related to diameter series 3 is : ƒb = 1.0
According to Fig. 5-13, coefficient ƒp for allowable rib surface pressure, related to
dmn = 80 × 1500 = 12 × 104, is : ƒp = 0.062
③Using equation (5-45), the allowable axial load
Fap is :
Fap = 9.8 ƒa・ƒb・ƒp・dm2 = 9.8 × 2 × 1.0 × 0.062 × 802 ≒ 7780 N
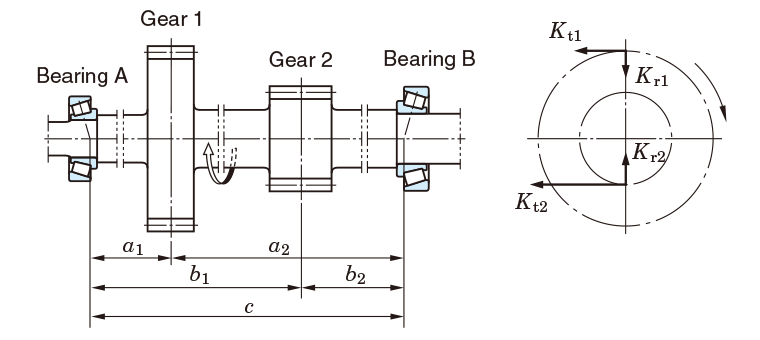
[Example 8] Calculation of service life of spur gear shaft bearings
(Conditions)
Tapered roller bearing
Bearing A:32309 JR
Bearing B:32310 JR
Gear type : spur gear (normally machined)
Gear pressure angle α1 = α2 = 20°
Gear pitch circle diameter
Dp1= 360 mm
Dp2= 180 mm
Transmission power W = 150 kW
Rotational speed n = 1000 min-1
Operating condition: accompanied by impact
Installation locations α1 = 95 mm ,α2 = 265 mm ,b1 = 245 mm ,b2 = 115 mm ,c = 360 mm
①Using equations (5-14) and (5-15), theoretical loads applied to gears (tangential load, Kt; radial load, Kr) are calculated.
[Gear 1]
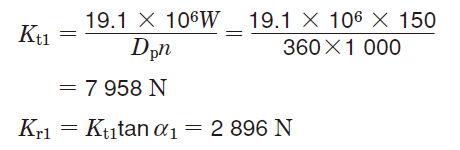
[Gear 2]
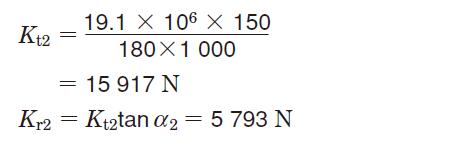
②The radial load applied to the bearing is calculated,
where the load coefficient is determined as ƒw = 1.5 from Table 5-6, and the gear coefficient as ƒg = 1.2 from Table 5-8.
[Bearing A]
Load consisting of Kt1 and Kt2 is :
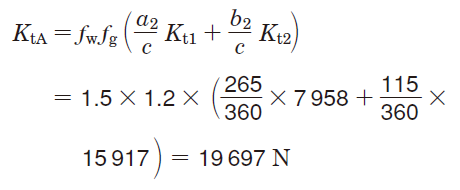
Load consisting of Kr1 and Kr2 is :
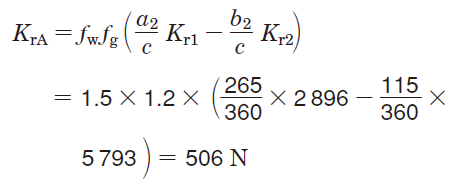
Combining the loads of KtA and em>KrA, the radial load (FrA) applied to bearing A can be calculated as follows :
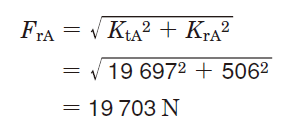
[Bearing B]
*Load consisting of Kt1 and Kt2 is :
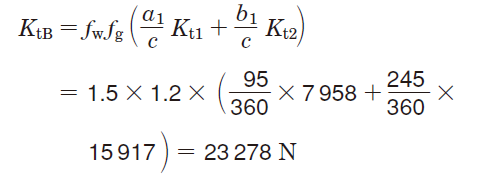
Load consisting of Kr1 and Kr2 is :
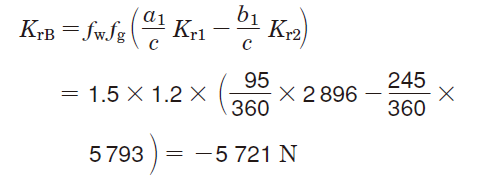
The radial load (FrB) applied to bearing B can be calculated using the same steps as with bearing A.
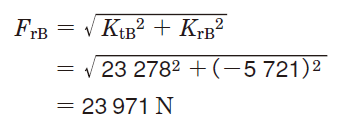
③The following specifications can be obtained from the bearing specification table.
| Basic dynamic load rating (Cr) | e | X1) | Y1) | |
|---|---|---|---|---|
| Bearing A | 183 kN | 0.35 | 0.4 | 1.74 |
| Bearing B | 221 kN |
[Note] 1) Those values are used, where Fa/Fr> e.
Where Fa/Fr≦ e, X = 1, Y = 0.
④When an axial load is not applied externally, if the radial load is applied to the tapered roller bearing, an axial component force is generated.
Considering this fact, the axial load applied from the shaft and peripheral parts is to be calculated :
(Equation 5-33, Table 5-9)
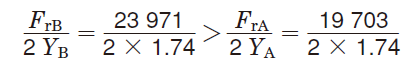
According to the result, it is clear that the axial component force (FrB/2YB) applied to bearing B is also applied to bearing A as an axial load applied from the shaft and peripheral parts.
⑤Using the values listed in Table 5-9, the dynamic equivalent load is calculated, where Ka = 0 :
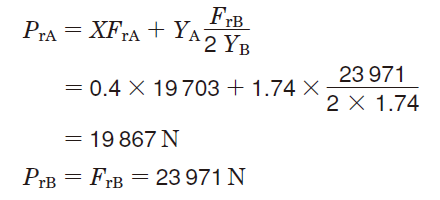
⑥Using equation (5-2), the basic rating life of each bearing is calculated :
[Bearing A]
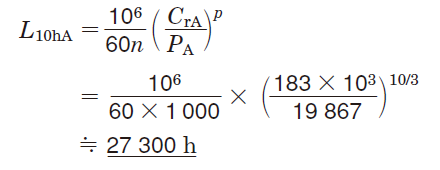
[Bearing B]
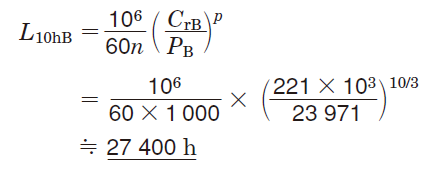
Reference
Using equation (5-11), the system service life (L10hs) using a pair of bearings is :