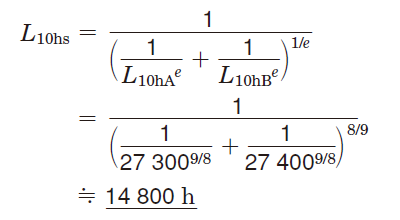〔例1〕軸受寿命(時間)の算定
(条件)
深溝玉軸受:6308
ラジアル荷重 Fr=3500 N
アキシアル荷重は作用しない。(Fa = 0)
回転速度 n=800min-1
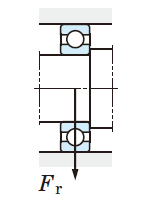
①軸受寸法表より基本動定格荷重(Cr)を得る。
Cr = 50.9 kN
②式(5-32)より、動等価ラジアル荷重(Pr)を求める。
Pr = Fr = 3500 N
③式(5-2)より、軸受寿命(L10h)を求める。
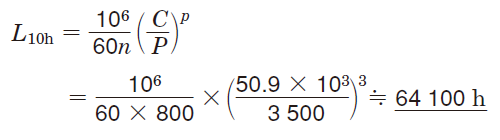
〔例2〕信頼度96%での軸受寿命(時間)の算定
(条件)
深溝玉軸受:6308
ラジアル荷重 Fr= 3500N
アキシアル荷重 Fa= 1000N
回転速度 n= 800min-1
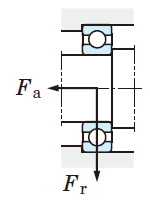
①軸受寸法表より、
基本定格荷重(Cr,C0r)ƒ0係数を得る。
Cr = 50.9 kN
ƒ0 = 13.2
C0r = 24.0 kN
ƒ0 Fa / C0r 値から比例補間法により求めた e 値をFa / Fr 値と比較することにより、X 及び Y 値を求める。
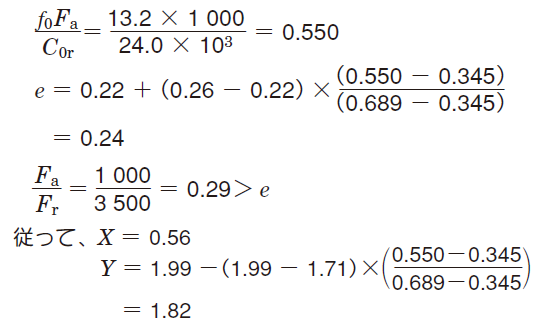
②式(5-32)より、動等価荷重(Pr)を求める。
Pr = XFr + YFa =(0.56 × 3500)+(1.82 × 1000)=3780 N
③式(5-2)より、信頼度90%での寿命(L10h)を求める。
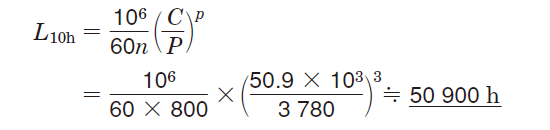
〔例3〕例2の条件でのαISO係数の算定
(条件)
油潤滑(細かなフィルタでろ過された油)
運転温度70℃
信頼度96%
④潤滑油の選定
軸受寸法表より、ピッチ径Dpw = ( 0 + 90)/2 = 65を得る。
dmn = 65 × 800= 52000。従い、潤滑剤のページ 『表12-8 使用条件による適正動粘度』からVG68選定。
⑤αISO係数の計算
運転温度70℃なので、潤滑剤のページ『図12-3 潤滑油の粘度と温度との関係(粘度指数 100の場合)』より運転時粘度 ν =20 mm2/s
図Aより、 ν1 = 21.7 mm2/s
κ = ν / ν1 = 20/21.7 = 0.92
油が細かなフィルタでろ過されているので表5-4からec は0.5~0.6。
厳しく見積もるためec = 0.5とする。
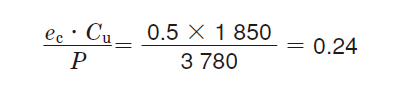
よって、図Bより
αISO = 7.7
⑥式(5-8)より、信頼度96%での寿命 Lnm を求める。表5-3より、α1 = 0.55とする。
L4m= α1αISOL10 = 0.55× 7.7 ×50900≒ 216000 h
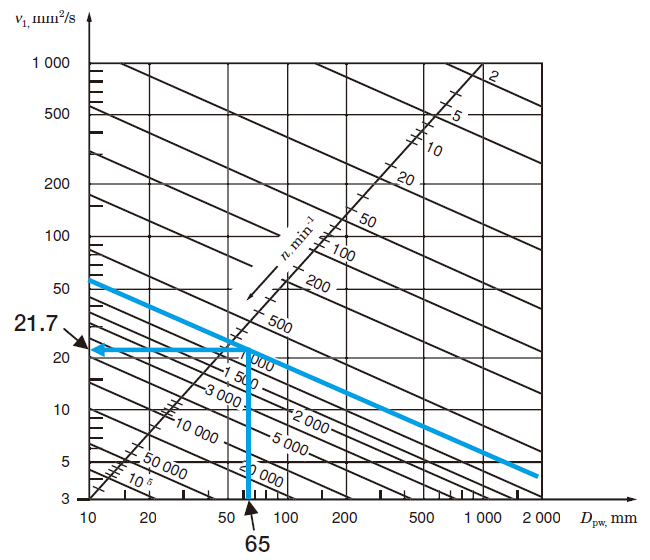
図A
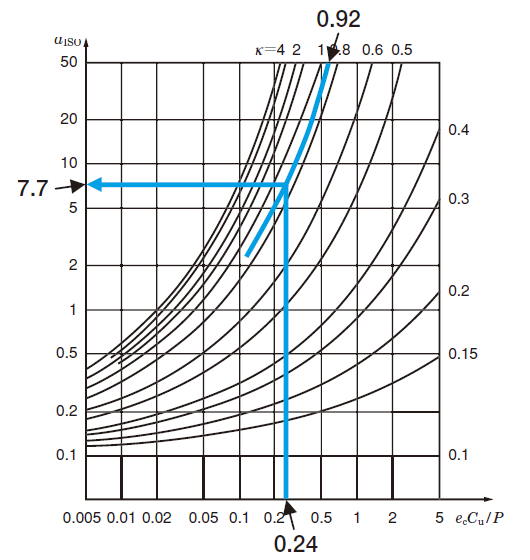
図B
αISO係数の計算は、WEBページでも計算可能です。
〔例4〕軸受寿命(総回転数)の算定
(条件)
円すいころ軸受
軸受 A:30207 JR
軸受 B:30209 JR
ラジアル荷重
FrA= 5200 N
FrB= 6800 N
アキシアル荷重 Ka= 1600 N
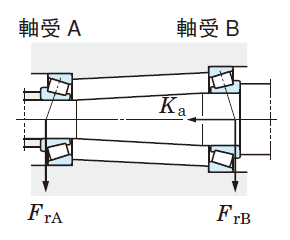
①軸受寸法表より、次の諸元を得る。
| 基本動定格荷重 (Cr) | e | X1) | Y1) | |
|---|---|---|---|---|
| 軸受A | 68.8 kN | 0.37 | 0.4 | 1.60 |
| 軸受B | 83.9 kN | 0.40 | 0.4 | 1.48 |
〔注〕1)Fa/Fr> e の場合の値を示す。 Fa/Fr≦ e の場合は X= 1,Y= 0
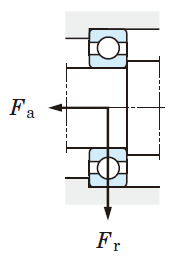
②円すいころ軸受にラジアル荷重が作用すると軸方向の分力が生じるので、これを考慮して軸系に作用するアキシアル荷重を求める。
(式5-33,表5-9)

③表5-9 より、動等価荷重(Pr)を求める。
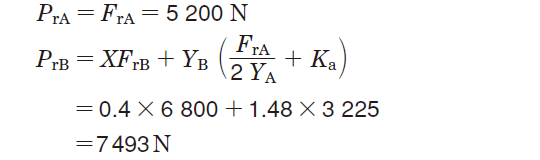
④式(5-1)より、各軸受の寿命(L10)を求める。

〔例5〕軸受寸法の選定
(条件)
深溝玉軸受: 62 系列
必要寿命時間: 10000 h 以上
ラジアル荷重 Fr= 2000 N
アキシアル荷重 Fa= 300 N
回転速度 n = 1600 min-1
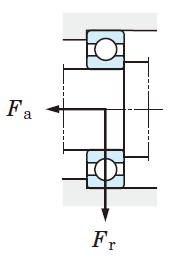
①動等価荷重(Pr)を仮算する。
Fa / Fr = 300/2000 = 0.15 となり、これは軸受寸法表のどの e の値よりも小さいので、Pr = Fr = 2000 Nと考えてよい。
②式(5-4)より、必要な基本動定格荷重(Cr)を求める。
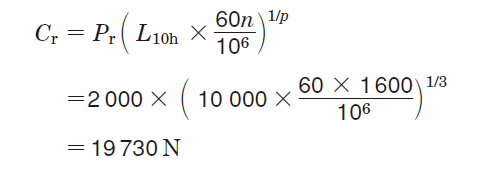
③軸受寸法表より、19730 N 以上の Cr を持つ 62 系列の軸受としては、内径 25 mm の 6205R を選定できる。
④6205 R の e 値を求めて、①の動等価荷重の値を確認する。
6205 R の C0rは9.3 kN、ƒ0は12.8であるから、ƒ0 Fa/C0r = 12.8 × 300/9300 = 0.413
次に、比例補間法によって e の値を求めると、
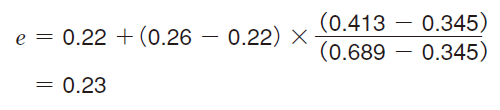
従って、Fa / Fr = 0.15 < e であるから Pr = Fr でよいことが分かる。
〔例6〕軸受寸法の選定
(条件)
深溝玉軸受: 63 系列
必要寿命時間: 15000 h 以上
ラジアル荷重 Fr= 4000 N
アキシアル荷重 Fa= 2400 N
回転速度 n = 1000 min-1
①動等価荷重(Pr)を仮算する。
Fa/Fr = 2400/4000 = 0.6 であり、軸受寸法表のe の値と比較すると相当大きいので、アキシアル荷重が動等価荷重に影響することが分かる。
従って、X = 0.56,Y = 1.6(Yの値の平均程度)と仮定すれば、式(5-32)より、
Pr = XFr + XFa = 0.56 × 4000 + 1.6 × 2400 = 6080 N
②式(5-4) より、必要な基本動定格荷重(Cr)を求める。
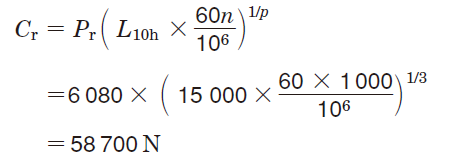
③軸受寸法表より、58700 N 以上の Cr を持つ 63 系列の軸受としては、内径 45 mm の 6309 を選定できる。
④6309 の e の値を求めて、動等価荷重及び基本定格寿命を確認する。
ƒ0Fa/C0r = 13.3 × 2400/29500 = 1.082 となるので、比例補間法により、e = 0.283,Y = 1.54を得る。
従って、Fa / Fr = 0.6 > e であるから
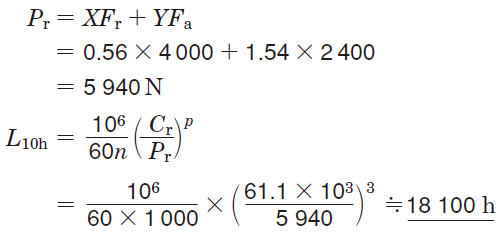
⑤同様に、6308 の基本定格寿命を求めると、L10h ≒ 11500 h となり、必要寿命を満足しない。
〔例7〕円筒ころ軸受の許容アキシアル荷重の算定
(条件)
単列円筒ころ軸受: NUP 310
回転速度 n = 1500 min-1
油潤滑
アキシアル荷重が間欠的にかかる。
①軸受寸法表より、NUP 310 の dm 値を求める。
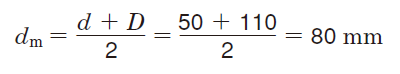
②式(5-45)における各係数を求める。
間欠負荷に対する係数 ƒa は、表5-11より
ƒa = 2
直径系列 3 に対する係数 ƒb は表5-12より
ƒb = 1.0
dmn = 80 × 1500 = 12 × 104 に対するつばの許容面圧に関する係数 ƒp は図 5-13 より、
ƒp = 0.062
③式(5-45)により、許容アキシアル荷重 Fap を求める。
Fap = 9.8 ƒa・ƒb・ƒp・dm2 = 9.8 × 2 × 1.0 × 0.062 × 802 ≒ 7780 N
〔例8〕平歯車軸に組込まれた軸受の寿命(時間)の算定
(条件)
円すいころ軸受
軸受 A:32309 JR
軸受 B:32310 JR
歯車の種類:平歯車(普通の機械加工)
歯車の圧力角 α1 = α2 = 20°
歯車のピッチ円直径
Dp1= 360 mm
Dp2= 180 mm
歯車の伝動動力 W = 150 kW
回転速度 n = 1000 min-1
運転状況:衝撃を伴う
取付け位置 α1 = 95 mm ,α2 = 265 mm ,b1 = 245 mm ,b2 = 115 mm ,c = 360 mm
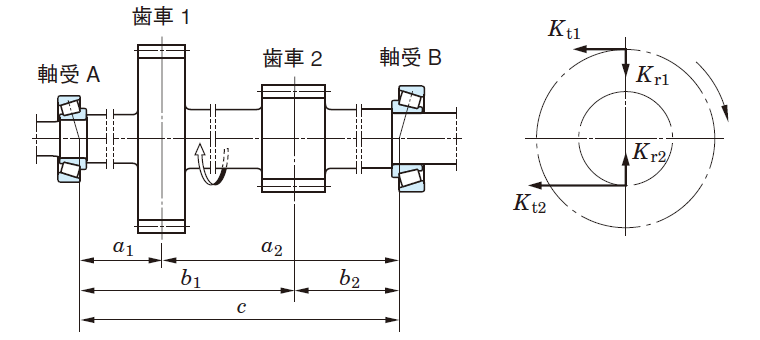
①式(5-14),(5-15)より、歯車に作用する理論上の荷重(接線方向荷重:Kt 及び 半径方向荷重:Kr)を求める。
〔歯車1〕
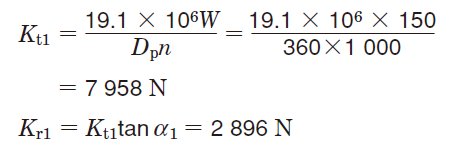
〔歯車2〕
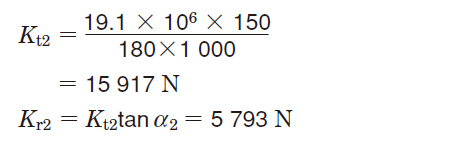
②軸受に作用するラジアル荷重を求める。
表5-6 より、荷重係数 ƒw = 1.5 及び 表5-8 より、歯車係数 ƒg = 1.2 とする。
〔軸受A〕
Kt1,Kt2 による荷重
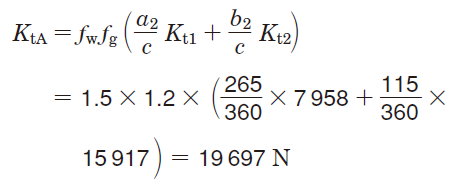
Kr1,Kr2 による荷重
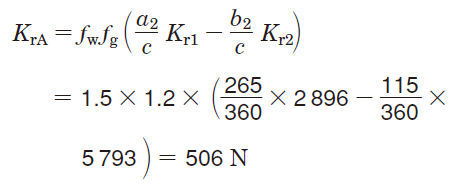
軸受A に作用するラジアル荷重(FrA)は KtA と KrA を合成することにより求められる。
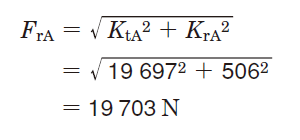
〔軸受B〕
Kt1,Kt2 による荷重
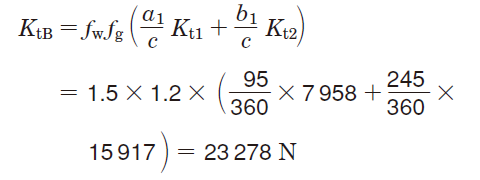
Kr1,Kr2 による荷重
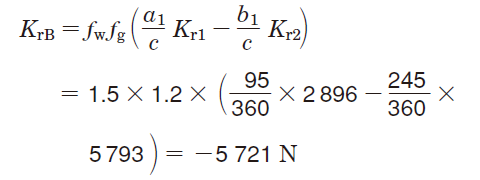
軸受B に作用するラジアル荷重(FrB)は軸受Aと同様の方法で求められる。
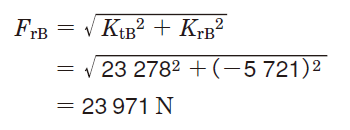
③軸受寸法表より、次の諸元を得る。
| 基本動定格荷重 (Cr) | e | X1) | Y1) | |
|---|---|---|---|---|
| 軸受A | 183 kN | 0.35 | 0.4 | 1.74 |
| 軸受B | 221 kN |
〔注〕1)Fa/Fr> e の場合の値を示す。Fa/Fr≦ e の場合は X=1,Y= 0
④外部からアキシアル荷重が作用しなくても、円すいころ軸受にラジアル荷重が作用すると軸方向の分力を生じるので、これを考慮して軸系に作用するアキシアル荷重を求める。
(式5-33,表5-9)
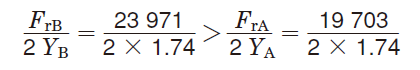
従って、軸受B の軸方向分力(FrB/2YB)が、この軸系のアキシアル荷重として軸受A に作用する。
⑤表5-9 において、Ka = 0 として動等価荷重を求める。
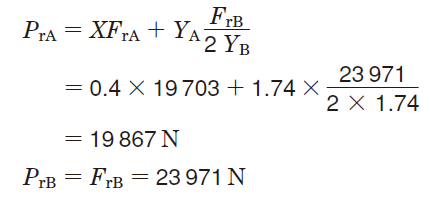
⑥式(5-2)より、軸受の基本定格寿命を求める。
〔軸受A〕
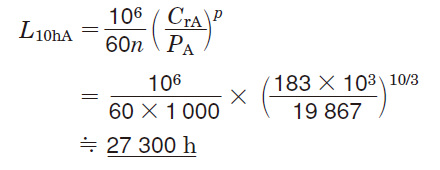
〔軸受B〕
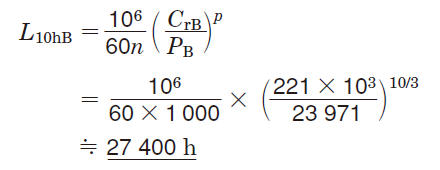
参考
式(5-11)より、2個の軸受のシステム寿命(L10hs)を考えると、